Gearing Systems
Nomenclature
Gearing systems are mechanisms that use gears to transmit motion, force, or power from one shaft to another. Gears are wheels with teeth around their circumference that mesh with other gears to create a rotational relationship between their axes. Gears can be used to change the speed, torque, or direction of rotation of an output shaft, as well as to transfer motion to non-parallel axes.
There are different types of gears that have different shapes, sizes, and arrangements of teeth. Some common types of gears are:
– Spur gears: These are the simplest and most common type of gear. They have straight teeth that are parallel to the axis of rotation and mesh with other spur gears on parallel axes.
– Helical gears: These are similar to spur gears, but their teeth are cut at an angle to the axis of rotation. This makes them quieter and smoother than spur gears, but also creates an axial thrust force along the shaft.
– Bevel gears: These are gears that have teeth cut on a conical surface. They are used to transfer motion between intersecting axes, such as in a car differential.
– Worm gears: These are gears that have teeth shaped like a screw thread. They mesh with a worm wheel, which is a gear with helical teeth. Worm gears can reduce the speed and increase the torque of an output shaft by a large amount, but they also have high friction and wear.
Some important terms related to gearing systems are:
– Pitch: This is the distance between two adjacent teeth on a gear, measured along the pitch circle.
– Pitch circle: This is the imaginary circle that passes through the points where the teeth of two meshing gears contact each other. The pitch circles of two meshing gears are tangent to each other.
– Module: This is the ratio of the pitch to the number of teeth on a gear. It is a measure of the size of the teeth and determines how well two gears mesh together. The module of two meshing gears must be the same.
– Gear ratio: This is the ratio of the number of teeth on the output gear to the number of teeth on the input gear. It determines how much the speed and torque of the output shaft change compared to the input shaft. A gear ratio greater than one means that the output shaft rotates slower and has more torque than the input shaft. A gear ratio less than one means that the output shaft rotates faster and has less torque than the input shaft.
– Gear train ratio: This is the overall ratio of the speed and torque of the final output shaft to the initial input shaft in a system of multiple gears. It is equal to the product of the individual gear ratios of each pair of meshing gears in the system.
– Pressure angle: This is the angle between the line of action and the common normal at the point of contact between two meshing teeth. The line of action is the line along which the force is transmitted between two meshing teeth. The common normal is the line perpendicular to both pitch circles at the point of contact. The pressure angle affects how much force is transmitted along the radial and axial directions of the shafts.
– Helical angle: This is the angle between the tooth face and an element of the pitch cylinder in a helical gear. It determines how much axial thrust force is generated by a helical gear pair.
Watch Professor Cummings provide a detailed example of each of these terms.
Specifying a Gear Train
To design a gearing system, one needs to follow these steps:
- Identify the input and output specifications, such as speed, torque, power, direction and type of motion.
- Choose the type of gears that suit the application, such as spur, helical, bevel, worm, planetary, etc. Consider the advantages and disadvantages of each type, such as efficiency, noise, strength, size, etc..
- Calculate the gear train ratio, which is the ratio of the number of teeth on the output gear to the number of teeth on the input gear. The gear ratio determines how much the speed or torque changes from the input to the output. Use the formula: gear ratio = output speed / input speed = input torque / output torque. If the gear train ratio is greater than about 1:10 you will likely need to use a compound gear train (multiple gear mates and shafts) to achieve the desired ratio.
- For each gear mesh in the ratio, select: pitch (or module), number of teeth (according to ratio determined earlier), and material for the gears, based on the required load capacity, wear resistance, durability, cost, etc. Use standard tables or formulas to find the pitch diameter, module, pressure angle, face width, etc. of the gears. Note, most gear manufacturers have calculators on their websites for finding appropriate gears strengths.
- Arrange the gears in a suitable configuration, such as parallel, intersecting or non-intersecting axes. Ensure that the gears mesh properly and have enough clearance and lubrication. Use sketches or CAD software to visualize and optimize the layout of the gearing system.
- Test and evaluate the performance of the gearing system, using analytical methods or experimental methods. Check if the output speed and torque meet the specifications, and if there are any problems such as vibration, noise, overheating, etc. Make adjustments or improvements as needed.
For example, suppose we want to design a gearing system that converts a high-speed low-torque input from an electric motor to a low-speed high-torque output for a conveyor belt. We can use the following steps:
- The input specifications are: speed = 1800 rpm (revolutions per minute), torque = 10 Nm (newton meters), power = 1885 W (watts), direction = clockwise, type of motion = rotary. The output specifications are: speed = 60 rpm, torque = 300 Nm, power = 1885 W (assuming 100% efficiency), direction = clockwise, type of motion = rotary.
- We can choose spur gears for this application, because they are simple, cheap and efficient. Spur gears have parallel axes and straight teeth that mesh along a line.
- We can calculate the gear ratio using the formula: gear ratio = output speed / input speed = input torque / output torque. Plugging in the values, we get: gear ratio = 60 / 1800 = 10 / 300 = 0.0333. This means that for every revolution of the input gear, the output gear makes 0.0333 revolutions. Note – This should be accomplished using a compound gear set with several gear mates not one. However, for the purposes of explanation we will consider a poor design with just one mate.
- We can select standard spur gears with a module of 2 mm (millimeters) and a pressure angle of 20 degrees. The module is the ratio of the pitch diameter to the number of teeth, and it determines how big or small the gears are. The pressure angle is the angle between the line of action and the tangent to the pitch circle, and it affects how much force is transmitted between the gears. Using standard tables or formulas, we can find that the pitch diameter of the input gear is 40 mm and it has 20 teeth. The pitch diameter of the output gear is 1200 mm and it has 600 teeth. The face width of both gears is 20 mm. Here, you can see why a compound gear is needed. For example, had we split the gear train into two meshes of 1:5 and 1:6 we could have a lot smaller total gear system. Start with gear one with 20 teeth and a module of 2 mm results in a diameter of 40 mm (20*2). This meshes with a gear of 100 teeth (1:5 ratio) and a pitch diameter of 200 mm. This second gear can be on the same shaft as the third gear which we can be the same size as gear 1 (20 teeth, 40mm diameter). Finally, this third gear meshes with a gear of 120 teeth and 240 mm diameter. The compound arrangement thus results in a total width of the gear train being much smaller than a single mesh.
- We can arrange the gears in a simple configuration with parallel axes and one pair of meshing spur gears. The center distance between the axes is half of the sum of the pitch diameters: center distance = (40 + 1200) / 2 = 620 mm. We can use a sketch or CAD software to draw and optimize the layout of the gearing system.
- We can test and evaluate the performance of the gearing system using analytical methods or experimental methods. We can use formulas or software to calculate the output speed and torque from the input speed and torque and compare them with the specifications. We can also measure them using instruments such as tachometers and dynamometers. We can check if there are any problems such as vibration, noise, overheating, etc., and make adjustments or improvements as needed.
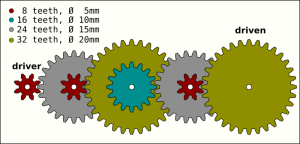
Determining a Gear Train RatioFinding the correct ratio for each mesh in a gear train requires deciding which type of gear train to use. |
Finding Gears from a Supplier CatalogThis is a walk through of a particular gear catalog. Most suppliers have similar websites and tools to aid in gear selection. |